 |
|
|
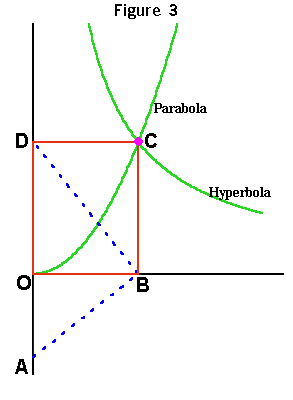
Menaechmus' Determination of Two Means by Conic Sections |
|
The intersection of an hyperbola and a parabola determine the magnitudes that double the cube. The parabola is formed from OA=1 and right angle ABD. The hyperbola is formed from the green rectangle OBCD which has an area of 2. From the parabola, OA:OB::OB:OD, or 1:OB::OB:BC. From the hyperbola, OB x BC = 2. Combining these two yields the proportion, 1:OB::OB:BC::BC:2. In other words, line OB will form a cube whose volume is 2 and BC will form a cube whose volume is 4. |