 |
|
|
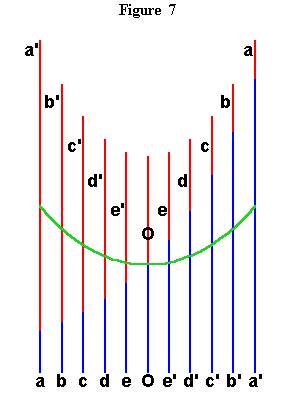
Leibniz's Construction of the Catenary |
|
The catenary is formed as the arithmetic mean between two curves which Leibniz called ``logarithmic,'' and are today called exponential. In the figure, the blue lines are spaced equally along a horizontal axis. The ``logarithmic'' curve is formed by the vertical lengths which are in geometric proportion. If OO=x0 =1, then ; e'=x1 and e= x-1=1/x1; d'=x2 and d=x-2=1/x2, etc. The catenary is formed by adding length e to e' and dividing the combined length by two; then adding length d to d' and dividing the combined length by two, etc. The points of the catenary are equal to (xn+1/xn)/2. |