Resumen electrónico de EIR, Vol. III, núm. 07
|
|||||
|
por Bruce Director
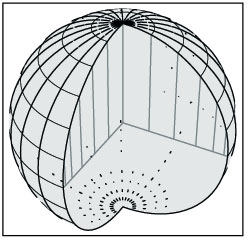
En su disertación de habilitación, Bernhard Riemann propuso establecer los fundamentos de la geometría sobre una base rigurosa: "Por ello, primero me propuse el problema de construir el concepto de una magnitud múltiplemente extendida partiendo de nociones generales de cantidad. De esto resultará que una magnitud múltiplemente extendida es susceptible a varias relaciones métricas, y que el espacio, de conformidad, sólo constituye un caso particular de una magnitud triplemente extendida. Una consecuencia necesaria de esto es que las proposiciones de la geometría no pueden derivarse de conceptos generales de cantidad, sino que esas propiedades por las cuales el espacio se distingue de otras magnitudes triplemente extendidas concebibles, sólo pueden tomarse de la experiencia". El programa de Riemann le plantea una paradoja a aquellos acostumbrados a la doctrina de Emanuel Kant y su forma más moderna y extrema, el existencialismo. ¿Cómo puede la experiencia determinar las proposiciones de la geometría? Kant insiste que: "El espacio no es un concepto empírico derivado de experiencias externas, pues a fin de que ciertas sensaciones refieran algo fuera de mí. . . debe presuponerse la representación del espacio. Por tanto, la representación del espacio no puede obtenerse de forma empírica a partir de las relaciones de la apariencia externa. Al contrario, esta experiencia externa es posible en lo absoluto sólo por esa representación. . . La geometría es una ciencia que determina las propiedades del espacio de forma sintética, e incluso a priori. En su origen, tiene que ser intuición; pues desde un mero concepto no puede obtenerse ni una proposición que vaya más allá del concepto, como pasa en la geometría. Las proposiciones geométricas son todas y cada una apodícticas, es decir, están ligadas con la conciencia de su necesidad; por ejemplo, ese espacio nada más tiene tres dimensiones. Tales proposiciones no pueden ser empíricas o, en otras palabras, juicios de la experiencia, ni pueden derivarse de ningún juicio tal". Kant no era muy original. Casi dos siglos antes Johannes Kepler (1571–1630), con su descubrimiento de la gravitación universal, ya había liberado a la ciencia de dogmas aristotélicos parecidos que, desde el asesinato de Arquímedes (212 a.C.) hasta el Renacimiento del siglo 15, esclavizaron a la civilización europea. A Kant lo desplegaron para poner de nuevo las cadenas. Esas doctrinas han demostrado que la experiencia (que para ellos se limitaba a la percepción sensorial) no puede decirnos nada del mundo físico. Por ejemplo, nuestra experiencia de fenómenos tales como el movimiento de los planetas y otros cuerpos celestes se limita a la percepción de los cambios de posición de puntos de luz dentro de una gran esfera de radio desconocido, cuyo centro es siempre la ubicación del observador. Para los aristotélicos, los movimientos reales así como los principios que los gobiernan son intrínsecamente desconocidos, de modo que deben referirse a algún conjunto de proposiciones determinado a priori, tales como los de Claudio Tolomeo, Nicolás Copérnico o Tico Brahe. A su vez, estas proposiciones se derivan en última instancia de axiomas, definiciones y postulados de corte euclidiano que, insistía Kant, son la única forma posible en que podemos concebir el espacio: "El espacio es una representación necesaria a priori que subyace a toda otra intuición externa. Nunca podemos representarnos la ausencia de espacio, aunque bien podemos pensar que está vacío de objetos. Por tanto, tiene que considerarse como la condición de la posibilidad de manifestaciones, y no como una determinación que depende de ellas. Es una representación a priori que necesariamente subyace a las manifestaciones externas". Según Kant, estas proposiciones no son en efecto verdaderas, no hacen juicios sobre los movimientos reales; son la forma mediante la cual deben representarse las manifestaciones, y no puede suceder nada que no sea posible bajo estas proposiciones. ¿Qué es la experiencia?Cuando empiezas a pensar en esto, te enfrentas cara a cara con la pregunta fundamental de la ciencia (y también de la política, la historia y el arte): ¿qué es la experiencia? ¿Es percepción sensorial? Ahí radica la trampa de Kant, porque si la experiencia se limita a la percepción sensorial, entonces ciertamente no puede decirnos nada de las proposiciones de la geometría. Como la sofistería de Kant insiste: "Si esta representación del espacio fuera un concepto adquirido a posteriori y derivado de la experiencia externa en general, los primeros principios de la determinación matemática no serían sino percepciones. Por consiguiente, todos compartirían el carácter contingente de la percepción; el hecho de que sólo debe haber una línea recta entre dos puntos no sería necesario, sino sólo lo que la experiencia siempre nos enseña. Lo que se deriva de la experiencia sólo posee una universalidad comparativa, a saber, aquello que se obtiene por inducción. Así, sólo debiéramos decir que, como se ha observado hasta ahora, no se ha encontrado ningún espacio que tenga más de tres dimensiones". No obstante, Riemann tenía algo muy diferente en mente cuando se refirió a la experiencia: "De esto surge el problema de buscar los hechos más simples a partir de los cuales pueden determinarse las relaciones métricas del espacio, un problema que no está bien definido en la naturaleza de las cosas; pues pueden plantearse varios sistemas de hechos simples que basten para determinar las relaciones métricas del espacio; el más importante para el propósito presente es el que Euclides sentó como base. Estos hechos, como todos los hechos, no son necesarios sino por una certeza meramente empírica; son hipótesis". Para Riemann, como para todo ser humano que no se haya autodegradado a una bestialidad aristotélico–kantiana, la experiencia no es la percepción sensorial; es la interacción activa de la mente con el universo del cual forma parte. Es, como insiste Platón, la formación de hipótesis, de hipótesis superiores y del proceso de hipotetizar la hipótesis superior. ¿El investigador investiga cómo investiga lo que está investigando? O, como para Apolo, quien canta en el himno de Percy Shelley, "Yo soy el ojo con el que el universo se contempla a sí mismo y se reconoce divino". Las proposiciones de la geometría pueden, y deben derivarse de esta clase de experiencia, y Riemann mejoró los métodos generales por los cuales se hace esto. Él divide esta tarea en dos pasos, los cuales descansan en los fundamentos establecidos por Carl F. Gauss. El primero, como se indicó arriba, es la determinación de la noción general de magnitud múltiplemente extendida. Aquí, Riemann cita el segundo tratado de Gauss sobre residuos bicuadráticos y su prueba del teorema fundamental del álgebra. En esos trabajos, así como en otras discusiones, Gauss atacó el enfoque de Kant como una "ilusión", y mejoró los conceptos de las investigaciones de los pitagóricos, Arquitas y Platón, de que la acción física, y no la intuición a priori, da origen a nuestro concepto de extensión, como lo ejemplifican los diferentes principios o poderes de acción física que extienden una línea, un cuadrado o un cubo. En cada forma de acción, la determinación de la característica esencial y distintiva, notó Riemann, siempre nos remite a "n" determinaciones de magnitud, donde "n" es el grado relativo del poder que gobierna la acción. Por ejemplo, a un cubo determinado por una magnitud triplemente extendida no puede determinarlo un cuadrado doblemente extendido, ni a un cuadrado una línea simplemente extendida. Sin embargo, existe aun otra consideración: "De ahí sigue, como el segundo de los problemas arriba planteados, una investigación de las relaciones de medición de las que es susceptible tal multiplicidad, también en condiciones que basten para determinar estas relaciones métricas. Estas relaciones de medición sólo pueden investigarse en nociones abstractas de magnitud y sólo pueden representarse de forma coherente en fórmulas; sin embargo, bajo ciertos supuestos, uno puede descomponerlas en relaciones que, por separado, admiten una representación geométrica, y de este modo es posible expresar los resultados del cálculo en términos geométricos. Por tanto, si uno quiere establecer bases sólidas, ciertamente es inevitable emprender una investigación abstracta en fórmulas, pero sus resultados permitirán presentarla en un ropaje geométrico. Los fundamentos de ambas partes están contenidos en el célebre tratado del consejero privado Gauss sobre las superficies curvas". Así, la cuestión del descubrimiento de una geometría física requiere resolver tanto las n determinaciones de magnitud como sus relaciones de medida. Ninguna de estas pueden darse a priori. Entonces, ¿cómo puede la experiencia cognoscitiva humana (en tanto opuesta a la kantiana) descubrir estos temas? Gauss, desde sus primeros trabajos bajo la tutela de Abraham Kästner y Hofrath von Zimmerman, reconoció que sólo los principios físicos, y no las definiciones, pueden sentar los fundamentos de la geometría, como por ejemplo la determinación de qué es una línea recta. De aquí, Gauss mostró que estos principios físicos determinan una curvatura característica de la que derivan las relaciones de medida de una superficie, y que estos principios generales de curvatura se expresan en las partes más pequeñas mediante las características de las "líneas más cortas", o geodésicas, de la superficie. Lo que resta por discutir es la inversión de este descubrimiento. ¿Cómo pueden determinarse los principios físicos de la curvatura de la superficie a partir de las características de las líneas geodésicas, medidas por pequeños cambios en esas geodésicas? El trabajo de Gauss en este problema inverso es de una importancia decisiva, porque esta es la forma de investigación que uno usualmente enfrenta en la ciencia, la política, la historia y el arte. No podemos conocer estos principios físicos mediante la percepción sensorial, pero sí percibir sus efectos mediante algún pequeño cambio mensurable por el cual, hipotetizando, podemos establecer los principios generales que determinan ese cambio. Kepler determinó los principios generales de curvatura de todo el sistema solar a partir de pequeños cambios que midió en la relación entre las órbitas de Marte y la Tierra. Godofredo Leibniz y Jean Bernoulli determinaron los principios generales de acción mínima a partir de pequeños cambios en la forma de una cadena suspendida en el aire. Gauss determinó la disonancia armónica del sistema solar, que Kepler había indicado, a partir de las diminutas mediciones de Giussepe Piazzi del arco de la órbita del asteroide Ceres. Lyndon LaRouche determinó la dirección general de la historia mundial a partir de cambios medidos en la perspectiva cultural y mental de la población tras la muerte de Fraklin Delano Roosevelt. Como Riemann indicó, es imposible explorar el trabajo de Gauss en esta dirección sin recurrir a conceptos abstractos expresados con fórmulas, pero estos resultados siempre pueden representarse de forma geométrica. Para propósitos pedagógicos, minimizaremos lo primero y recalcaremos lo último, pero es inevitable hacer una referencia limitada a fórmulas, y siempre vendrá acompañada de la representación geométrica apropiada. La magnitud simplemente extendida Para empezar a dominar los principios involucrados, toma el caso simple de una línea. Cuando se considera como una magnitud simplemente extendida, una línea puede aumentar o disminuir sólo mediante la acción a lo largo de su longitud, es decir, de un lado a otro. Tales cambios sólo pueden medirse por incrementos de más o menos, y expresarse con números racionales. Sin embargo, cuando se considera que a esa línea la genera una magnitud doblemente extendida, como la diagonal de un cuadrado o un rectángulo, sus incrementos o decrementos se miden con un conjunto de relaciones totalmente diferente, como demuestra Platón en los diálogos Menón y Teetetes. En este caso, la línea aumenta o decrece sobre su longitud, pero sólo de una forma coherente con cambios en la longitud del lado del cuadrado o rectángulo. Estos cambios no pueden medirlos las simples ideas de más o menos, como lo expresan los números racionales. Más bien expresan la suerte de relación conocida como el "teorema de Pitágoras" que, como Pitágoras y Platón subrayaron, es inconmensurable con magnitudes simplemente extendidas. Dibuja un rectángulo y llama a la longitud de uno de los lados "x" y a la del otro "y". Por el teorema de Pitágoras, la longitud de la diagonal "s" puede medirse como la raíz cuadrada de la suma de los cuadrados de los dos lados, o en taquigrafía: s=V¯(x2+y2). Si la diagonal se extiende una pequeña distancia "ds", los lados del rectángulo aumentarán en pequeñas cantidades proporcionales "dx" y "dy" (ds, dx y dy son la notación de Leibniz para estos incrementos infinitesimales, que él llamó diferenciales). Si esta acción tiene lugar en un plano euclidiano, entonces ds, dx y dy expresarán la relación pitagórica ds=V¯(dx2+dy2). Así, a diferencia de las versiones de los libros de texto, la relación pitagórica no es una fórmula arbitraria; expresa una relación característica de cierta clase de superficie: un plano euclidiano. De manera inversa, si un proceso físico se mide mediante la relación pitagórica expresada arriba, esa acción ocurre en un plano euclidiano. Esta relación física mensurable, no la máxima de Kant de la certeza a priori, es la única realidad de un plano euclidiano. Y, ya que las medidas físicas del mundo real expresan una relación diferente, la realidad física de un plano euclidiano, no sólo es innecesaria, sino ilusoria. Pero, si nuestra experiencia cognoscitiva, es decir, la medición física, determina que la relación pitagórica es insostenible, entonces, ¿qué relación expresa una magnitud doblemente extendida? Un kantiano tendrá un arrebato de ira ante esta paradoja. Kant insiste que el espacio euclidiano es la única forma posible en que uno puede pensar acerca del espacio; por consiguiente, para el kantiano el espacio euclidiano tiene que ser el único espacio posible. Y así, los kantianos exigirán que se trate al mundo como si fuera euclidiano, aunque las mediciones físicas nos digan lo contrario. Estafadores en la tradición de Galileo, quien intentó encajar la curva catenaria en una parábola, no tendrán problema con esto. Sugerirán mediciones físicas restrictivas para regiones lo bastante pequeñas, de modo que la desviación de la relación pitagórica esté por debajo de los errores de medición. Sin embargo, este truco es sólo un autoengaño, pues la desviación de lo plano, no importa que tan pequeña parezca, sigue existiendo, y tarde o temprano será imposible pasar por alto el error de juicio sobre ese engaño. Por supuesto, Gauss rechazó tales necedades. Él reconoció que la relación pitagórica, como la expresa la geometría euclidiana, no era "sacrosanta"; más bien era sólo un caso especial de un principio más general. En vez de aferrarse al caso especial, Gauss descubrió los fundamentos del principio general. Para entender el descubrimiento de Gauss, es pedagógicamente eficiente el trabajar varios ejemplos y luego abstraer de ellos el principio general que entra en acción. Comenzando con el caso de la esfera celeste físicamente determinada. A esta superficie la determina, en términos físicos, la posición del observador y la dirección de la atracción gravitacional. La primera determina el centro de la esfera, y la segunda los polos y el horizonte. Si nos ceñimos a la constricción de Kant, de que sólo podemos pensar en el espacio como extendido a infinito en tres dimensiones, entonces esta esfera aparece como un gran objeto rodeado de espacio vacío. Pero Gauss entendió la esfera celeste como una multiplicidad de acción física producida por dos ángulos mutuamente interdependientes: los ángulos a lo largo del horizonte ("latitud"), y los perpendiculares a él ("longitud"). Todas las posiciones en la esfera celeste pueden determinarse con estos dos parámetros físicos (así, para la esfera, n=2, en términos de las n determinaciones de magnitud de Riemann). A partir de esta relación Gauss construyó lo que se conoce como "fórmula paramétrica", en la que estos dos parámetros expresan por completo la superficie de la esfera.
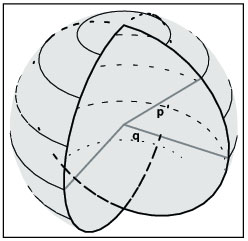
Todos los círculos longitudinales tienen un centro común, es decir, el observador. Las posiciones sobre cualquiera de estos círculos puede determinarlas una función del ángulo que forma el horizonte con el cenit. Si a este ángulo se le llama "p", entonces cualquier posición sobre un círculo de longitud puede determinarse como una función del seno y el coseno del ángulo "p" (ver figuras 1a, b y c).
Cada uno de estos círculos de longitud puede distinguirse de otro por otro ángulo, al medirse alrededor del horizonte. Si se llama "q" a ese ángulo, entonces las posiciones alrededor de este círculo pueden determinarse como una función del seno y el coseno del ángulo "q".
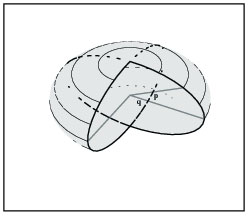
Así, para todas las posiciones sobre un solo círculo de longitud, "q" es constante y "p" varía, al tiempo que para todas las posiciones sobre un círculo de latitud, "p" es constante y "q" varía. Sin embargo, hay una diferencia significativa entre ambas clases de círculos. El centro de todos los círculos de longitud es el mismo que el de la esfera, en consecuencia, todos los círculos de longitud son círculos máximos. Pero los círculos de latitud se vuelven más pequeños en tanto se alejan del horizonte y se acercan a los polos. Qué tanto empequeñecen, es decir, qué tan cerca están de los polos, es una función del ángulo p. En la geometría de la esfera el radio de los círculos de latitud es proporcional al coseno del ángulo "p" (ver figura 2).
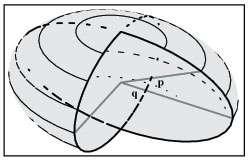
A partir de esto, todas las posiciones sobre una esfera pueden reducirse a determinaciones de los dos parámetros "p" y "q", que reflejan la curvatura física de la esfera.[1] La caja vacía, en la que Kant insiste, simplemente desapareció, quizás en los rincones vacíos de su cerebro. Luego Gauss investigó la relación entre la longitud de una geodésica arbitraria de la esfera y los ángulos "p" y "q", para determinar una forma de medir los principios generales de curvatura de la superficie a partir de pequeños cambios registrados en la geodésica. La 'esférica pitagórica'Para esto, Gauss estableció una forma más general de la relación pitagórica. En el caso de la esfera, una línea geodésica puede considerarse como una diagonal de un rectángulo esférico, cuyos lados son círculos de longitud y latitud. Pero, a diferencia de la pitagórica en el plano euclidiano, la relación entre los lados de los rectángulos esféricos cambia según su posición con respecto al horizonte y los polos. Específicamente, los lados latitudinales se encogerán por un factor proporcional al coseno del ángulo "p", en tanto los lados longitudinales crecen hacia los polos (ver figura 3).
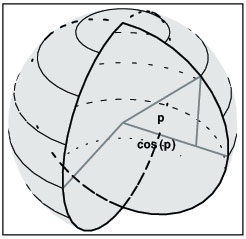
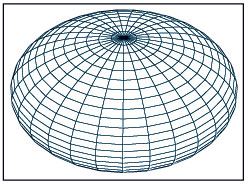
Así, la "esférica pitagórica" tiene que medir, no sólo la relación de la diagonal con los lados, sino también el cambio en esta relación al tiempo que la relación entre los propios lados cambia. Con esto, Gauss demostró que la forma de la pitagórica esférica es que la longitud de la geodésica "ds" = V¯((cos[p])2dp2+dq2), donde "ds" es el cambio en la longitud de la diagonal, y "dp" y "dq" son los cambios en la longitud y la latitud. El coeficiente cos[p]2 expresa la disminución de las líneas de latitud en tanto se acercan a los polos. De ahí que si uno hace mediciones físicas a lo largo de lo que parece ser una "línea recta", y la relación medida corresponde con esta "pitagórica esférica", entonces esa "línea recta" es una geodésica sobre una esfera. Para desarrollar más esta idea, sigue por la misma vena los siguientes dos ejemplos: el esferoide y el elipsoide. Para el esferoide, puede construirse una fórmula paramétrica que exprese la relación geométrica de que las líneas de latitud se acortan en tanto se aproximan a los polos, al tiempo que las de longitud se alargan (ver figura 4). En este caso, el "esferoide pitagórico" tiene que expresar la relación entre la longitud de la geodésica, "ds", y la relación cambiante entre las longitudes de los círculos de latitud y las elipses de longitud. Esto produce una fórmula un poco más complicada para el "esferoide pitagórico", pero su representación geométrica puede verse en la figura siguiente.
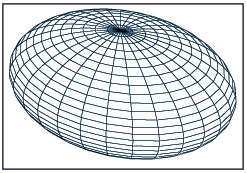
Por inversión, si las mediciones físicas sobre una "línea recta" reflejan la relación que expresa el "esferoide pitagórico", esa "línea recta" tiene que ser una geodésica sobre un esferoide. En el elipsoide, la relación entre los lados de los "rectángulos elipsoidales" cambia en tanto se mueven hacia los polos y también alrededor en dirección latitudinal (ver figura 5). Usando el método de Gauss, es posible calcular una fórmula para este "elipsoide pitagórico" que nos permite hacer la misma suerte de determinaciones sobre los principios generales de curvatura de pequeños cambios en la medición de la "geodésica elipsoidal".
En su tratado sobre superficies curvas, citado por Riemann en su disertación de habilitación, Gauss desarrolló una forma general de la pitagórica que expresaba la relación entre la línea geodésica y las dos determinaciones de magnitud de esa superficie. Para propósitos puramente ilustrativos, la forma generalizada de la pitagórica de Gauss es ds=V¯Edp2+2Fdpdq+G2dq2, donde E, F y G son funciones que expresan la relación cambiante de los dos parámetros de la superficie. E expresa la función por la que "p" cambia con respecto a "q"; G expresa la función por la que "q" cambia con respecto a "p"; y F expresa al función por la que el área del rectángulo cambia en relación a los cambios en "p" y "q". Para el plano euclidiano, la pitagórica de Gauss se reduce a la forma que conocemos. Como Riemann indicó, esta relación en su forma más general la expresa la fórmula anterior, pero, como en los ejemplos previos, sus resultados siempre pueden representarse en términos geométricos. Con este fundamento establecido por Gauss, Riemann fue más allá en determinar una idea aun más general de una pitagórica, no sólo para superficies, sino para multiplicidades de n determinaciones de magnitud. Esto lleva a esferas aun más interesantes, tales como con la que uno topa al investigar procesos físicos en lo muy pequeño y en lo muy grande, o en el dominio biótico, donde la característica de la geodésica cambia de forma no uniforme. Sin embargo, para llegar a esto, primero tenemos que dominar los fundamentos de Gauss y Riemann, con alguna ayuda de las ideas del arte clásico, tales como los últimos cuartetos de cuerdas de Beethoven. ____________________________________________________________________ [1] Para quienes quieran saberlo, una fórmula paramétrica para la esfera es cos[q] cos[p], sen[q] cos[p], sen[p]. Para el esferoide y el elipsoide, cada dirección se multiplica por un factor simple. |
|||||