Recuadro 19: Cuando agarres a esta ‘nena’, recuerda ser ‘tangentil’

regrese al artículo

regrese al inicio

Lea El principio del ‘poder’ en formato PDF

“Lo ingenioso de esta curva sólo se equipara a la simplicidad de su construcción, lo que la convierte en la principal de entre todas las curvas trascendentales”.

—Leibniz, Sobre la curva catenaria, 1691.

Leibniz, a sabiendas de que el orden del universo se desarrolla de conformidad con la perfección, por la cual la simplicidad de sus medios produce los logros más fecundos, procuró lograr que la condición de la humanidad fuera coherente con la realidad descubrible de semejante universo.

La simplicidad de sus medios sale a relucir en la investigación de Leibniz de la catenaria, una curva que definió expresaba la “acción mínima”. Esta curva pende al universo en suspensión perfecta entre a cada punto infinitesimal y, por ello, expresa de la forma más sencilla la trayectoria en la que la gravedad ordena al mundo material. La productividad de la catenaria sobrepasa la de todas las demás curvas, por su poder de generar todos los poderes algebraicos a partir de sí misma, demostrando así, de verdad, el poder de lograr el efecto más fecundo.

Su naturaleza constantemente cambiante es la mejor expresión del cálculo de Leibniz, en el cual todo movimiento y materia se guía constantemente, no por la percepción sensorial o conectando puntos y determinando ecuaciones algebraicas, sino mediante un conjunto de relaciones no vistas que exigen que se mantengan en cada parte, como en una curva que cambia su trayectoria, apuntando así a un principio físico no visto que existe universalmente a lo largo de toda la curva. Estos principios, que se reflejan como una relación orientadora, existen hasta en el intervalo de cambio más pequeño, como ocurre a lo largo de la catenaria, donde la acción mínima se mantiene hasta en el punto que los empiristas llaman nada o cero: el punto exactamente en lo más bajo de la cadena.

De modo que Leibniz, dejándole el mundo de caos inmutable de la percepción sensorial a las bestias, resolvió una paradoja de la percepción sensorial que parecía irresoluble, en la cual un universo que cambia de manera constante, tal como una trayectoria de curvatura constante, puede conocerse mediante puntos paradójicos infinitesimal mente pequeños, que son los más simples, pero también los que tienen más poder. Por consiguiente, al descubrir la razón de la curva catenaria, abriendo todo un nuevo campo de la ciencia, Leibniz le demostró experi mentalmente a la humanidad que el universo es el de un Creador perfecto, diseñado para que la mente humana descubra sus verdades eternas. Aunque cuando frecuentemente lo ocupaban “responsabilidades de una naturaleza completamente diferente”, esto es, el lanzamiento de un Renacimiento político mundial que alcanzó las costas de Norteamérica y se extendió tan lejos como a China, Leibniz vio que mejorar el método por el cual la humanidad podía descubrir principios y aplicarlos a elevar aun más la perfección y el poder de la mente humana, resultaba en avances profundos para toda la especie humana y que, por ende, era el único medio para cambiar el estado de la humanidad. Éste es el poder de la catenaria.

La curvatura de la catenaria

“El primero que pensó en esta curva, que la forma una cuerda libremente suspendida o, mejor, una cadena delgada no elástica, fue Galileo. Sin embargo, él no comprendió su naturaleza; al contrario, afirmó que es una parábola, cosa que sin duda no es. Joaquín Junge descubrió que no es una parábola, como Leibniz advirtió, mediante cálculos y sus muchos experimentos. Sin embargo, no indicó la curva correcta para la catenaria. Por tanto, le correspondió a nuestra época solucionar este importante problema”.

—Johann Bernoulli, Clases de cálculo integral, 1691.

La catenaria es la curva que forma una cadena suspendida; la atracción de la gravedad y la tensión horizontal actúan sobre su curvatura constantemente no constante. Su cambiante relación vertical–horizontal sólo puede deter minarse físicamente mediante esas dos fuerzas, y no puede expresarse en términos algebraicos en ningún sistema de coordenadas cartesiano. ¿Es cog noscible el poder único que determina la interacción de estas fuerzas?

Suspende una cadena entre tus manos. Manteniendo la cadena en una posición, pídele a alguien que agarre la cadena desde una parte más baja. ¡Suelta lo que sobra de la cadena! ¿Cambia su estructura? No. El peso total entre tus manos cambia, pero no la estructura de la cadena. Aunque la fuerza vertical se incrementa a medida que la cantidad de cadena aumenta, la fuerza horizontal permanece constante; esto puede descubrirse encontrando la fuerza horizontal en lo más bajo de la catenaria y observando el efecto conforme remueves segmentos de cadena. ¿Cambia la fuerza horizontal (ver figura 1)?

La tensión horizontal constante y la fuerza de gravedad vertical tienen una relación cambiante y no vista, a medida que cambias la posición de tus manos sobre la cadena. Para encontrar cómo estas fuerzas determinan la curva, es necesario usar más que los sentidos.

Por tanto, procediendo hacia lo no visto, remueve una parte de la cadena y remplázala con un peso que penda tangente a la curva. ¿Qué observas? Si tus mediciones son correctas, los eslabones que sostienen el peso, igual a la cadena removida, no se mueven ni se percatan del cambio. Por consiguiente, como el peso de la cadena ejerce su acción en los puntos tangenciales y la fuerza vertical del peso es igual, sin importar si tienes a la catenaria o una cantidad de peso suspendida en la intersección de sus tangentes, la relación no vista entre las fuerzas horizontal y vertical que actúan para determinar la curvatura de la cadena, pueden ahora descubrirse y medirse con precisión usando este método de las tangentes (ver figura 2).

Suspende ahora un peso sobre una cuerda. Si no se balancea de un lado a lado, es claro que la tensión horizontal es constante, en tanto que la fuerza vertical sobre cada lado de la cuerda varía conforme sus ángulos cambian (ver figura 3).

Mantén inmóvil el peso, y rota una de las cuerdas de forma perpendicular a la atracción de la gravedad (ver figura 4).

En este momento del experimento surge una singularidad de las relaciones físicas: la fuerza que tira en ese extremo de la cuerda sólo es horizontal, sin ningún componente vertical. Sólo en este punto singular se encuentra que la relación entre la fuerza horizontal constante y la fuerza del peso vertical que tira hacia abajo corresponde a la proporción entre los senos de los dos ángulos a y b, que corresponden a las longitudes vertical y horizontal X y Y (ver figura 5).

FIGURA 1	FIGURA 2
FIGURA 3	FIGURA 4
FIGURA 5

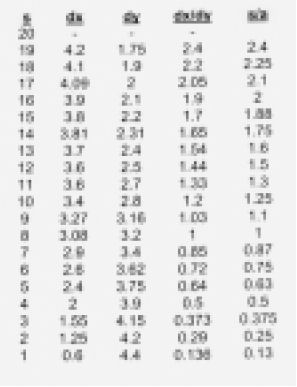
Como la cadena o el peso que pende de las tangentes tiene el mismo efecto sobre los eslabones tangenciales, la relación entre el peso total E y la fuerza horizontal en B puede expresarse de modo similar como la relación entre toda la cadena AB y la longitud de la cadena que aparece en la figura 1, cuyo peso es igual a la fuerza horizontal en lo más bajo. Por ende, el cambio vertical y horizontal que se expresa como el largo X y el largo Y puede expresarse en una relación proporcional con la longitud AB y a. X/Y=AB/a.

En otras palabras, la relación de fuerzas se transforma de vuelta a la relación que corresponde a nuestra longitud original de la cadena catenaria y, por consiguiente, se descubre que las fuerzas físicas son proporcionales al cambio vertical–horizontal.

Pero, ¿es esta relación constante a todo lo largo de la cadena? Usando el método del cálculo de Leibniz, un cambio infinitesimalmente pequeño de la tangente resultará en un cambio infinitesimalmente pequeño en X y Y, expresando la misma relación. Por tanto, la relación de las dos fuerzas es precisamente proporcional al cambio de X y Y en cada punto; en otras palabras, un punto infinitesimalmente pequeño expresa la relación que guía a toda la curva.

La característica física no vista se manifiesta por medio de un solo “punto”. Este punto hace lo que ningún otro punto sobre la catenaria. Al actuar como una verdadera singularidad de la geometría física, expresa con más claridad el poder físico no visto que ordena la curvatura de la catenaria.

La figura 6 demuestra este descu brimiento para 20 puntos de tangencia, donde S es considerado como longitudes diferentes de la catenaria y a es la constante que equivale a 8 sujetapapeles. Aquí, al revisar los datos, observa la relación que existe aun cuando los parámetros cambian constantemente. Hipotetiza qué relación exige mantenerse, aunque aparezca cambiando en cada expresión diferencial. ¿Puede conocerse esto de otra forma que no sea su relación física?

FIGURA 6

Para animar aun más esta nueva idea, examinando estas fuerzas físicas sólo como longitudes cambiantes, se construyó una prueba del principio, usando una máquina–herramienta, para demostrar de forma continua la expresión diferencial S/a=dx/dy. Las mediciones tomadas aparecen en la figura 7.

FIGURA 7

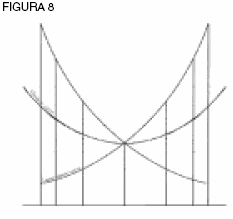
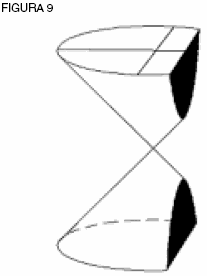
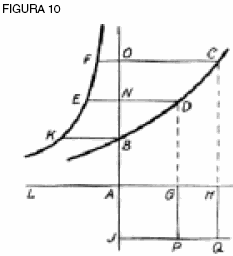
La función logarítmica natural

Repitiendo lo que se dijo antes, la curva catenaria no puede conocerse a partir de ninguna función algebraica. Leibniz, al buscar un “tipo de expresión, así como la mejor de todas las construcciones posibles para las trascendentales”, se vio conducido a un “dominio superior para el que necesitaban abrirse nuevas sendas”. Él encontró que la catenaria podía construirse como la media aritmética entre dos curvas logarítmicas, una construida de manera inversa a la otra. Así, la catenaria es una función de dos funciones no algebraicas (ver figura 8).

¿De qué construcción física se derivan estas dos curvas logarítmicas inversas?

Prueba con un cono doble de 90° cortado de forma perpendicular a la base. Esto crea una hipérbola (ver figura 9).

Regresando a las clases de Bernoulli sobre integración, uno ve que él demuestra que la hipérbola crece en área de manera aritmética, en tanto que la longitud crece geométricamente. De ahí que, él construye la esencia de la hipérbola equilátera: la curva logarítmica natural, una curva de crecimiento aritmético en una dirección y de crecimiento geométrico en la otra, con una subtangente de 1 (ver figura 10).

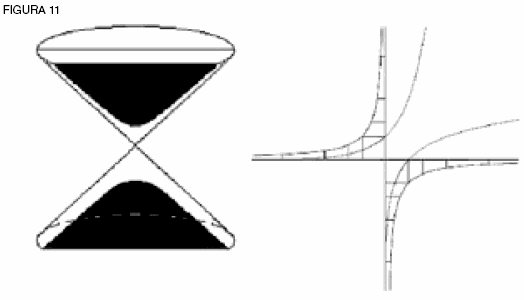
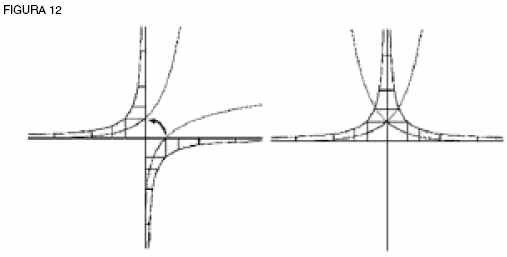
Ahora, regresa al cono doble y construye una curva logarítmica a partir de las curvas de la hipérbola a cada lado. ¿Son éstas las dos curvas que Leibniz usa para construir la catenaria? ¿Cómo podemos reproducir su construcción con nuestras dos curvas logarítmicas invisibles a lados opuestos del cono? ¿Qué se requiere para llevar estas curvas a mantener una relación inversa (ver figura 11)?

Para construir la relación de las curvas logarítmicas naturales que Leibniz diseñó, una curva tiene que rotar alrededor del punto cero sobre el eje, o sea, el vértice del cono doble. ¿Qué tanto? ¡Una cantidad “imaginaria” (ver figura 12)!

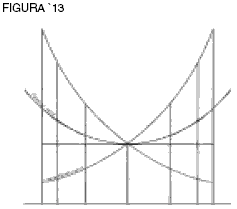
Así se encuentra la construcción de Leibniz, en un nuevo dominio que existe paradójicamente desde la perspectiva del cono percibido por los sentidos. Como Leibniz proclamó: “El Espíritu Divino encontró una manifestación sublime en esa maravilla de análisis, ese portento del mundo ideal, lo anfibio entre ser y no ser, a lo que llamamos la raíz imaginaria de la unidad negativa”.

¿Cómo descubrió esto Leibniz?

Investiga más de cerca esta construcción. ¿Cuál es la media geométrica entre las dos funciones logarítmicas? Bueno, la altura de la curva logarítmica bajo la catenaria es a la altura de uno, lo que uno es a la altura de la curva logarítmica sobre la catenaria. En otras palabras, la media geométrica es la tangente al punto más bajo de la catenaria, que es, irónicamente, el punto que delata el poder físico no visto que genera la curvatura de la catenaria (ver figura 13).

“Aunque mis manos estaban atadas”, escribió Leibniz en 1691, “y no podía ocuparme de esto como debí hacerlo, había un dominio superior para el que necesitaban abrirse nuevas sendas; de modo que, a mi ver, esto era lo importante: a saber, que el caso de desarrollar métodos siempre es más decisivo que los problemas particulares, aunque es lo último lo que por lo general gana aplausos”.

—Michael Kirsch y Aaron Yule.

—Traducción de Zaid Jaloma Minjares.