Estudios estratégicos
Recuadro 2: La construcción de
volúmenes
regrese al artículo
regrese al inicio
Lea El principio del ‘poder’ en formato PDF
¡Construye!
es la construcción. La construcción pone a prueba la viabilidad de aquellas ideas que la mente considera como las mejor concebidas: ¿son realmente de extracción legítima, o algún adúltero te agarró con la guardia baja y lo adulteró todo?
Quizá pienses: “¡Ah, esto lo conozco! Es fácil. . .” Pero cuando tratas de llevar la idea de tu mente al mundo de lo visible... bueno, ¡está lejos de ser tan simple como pensaste! La mente se apresura, desembarazada del mundo material, capaz de concebir sistemas perfectamente congruentes, diseños gloriosos, maquinaciones elaboradas... que poco tienen que ver con la realidad. El cuerpo, entre tanto, que carga con el lastre de su propia carne, se bate en el fango, capaz apenas de procurar el placer sensual de un cerdo. ¿Dónde está la conexión?
La construcción es la media entre la mente y el cuerpo; es el medio para producir música mediante la armonía de estos dos elementos diametralmente opuestos. Es el único medio para investigar la realidad. Si aceptas el reto que plantea Lyndon LaRouche aquí, si te ensucias las manos en busca de la solución, es probable que generes una idea directamente relacionada con la que determina lo que ahora escribo en mi intento de comunicar los frutos que obtuvimos al bregar con el desafío de LaRouche. Es probable que te rías, como nosotros, y como sospecho que LaRouche se rió al escribir el problema como lo hizo. En unas cuantas palabras plantea una investigación que toma muchas horas y, en realidad, mucha gente investigar como es debido. Y, por si fuera poco, incorpora un elemento de imposibilidad aparente que reconocimos de inmediato.
Primero, LaRouche nos pide que pensemos en el volumen de agua que podría contener un cubo, “en comparación con la esfera o el toro pertinentes de la misma capacidad”. Si con eso de veras quiere decir lo que dijo, lo que nos pide es la “cubicación de la esfera”: nos pide que generemos un volumen cúbico igual al de la esfera. Sin duda, éste no es un problema menor que el de la cuadratura del círculo, y, de hecho, es mucho mayor.
La cuadratura del círculo es el proceso de irse aproximando cada vez más a la longitud del perímetro del círculo, dibujando polígonos inscritos y circunscritos con un número de lados siempre en aumento, como lo hizo Arquímedes. La idea del proceso es crear un cuadrado cuya área sea exactamente igual a la del círculo. Arquímedes le aplicó al círculo un método asociado con Eudoxo —un amigo de Platón—, llamado “exhaustivo”. El método exhaustivo había funcionado bien en ofrecer resultados precisos para otros problemas, como el de la cuadratura de la parábola, y problablemente se aplicó, con un efecto parecido, a algunos de los problemas volumétricos que encontramos a continuación.
Pero Nicolás de Cusa demostró que una verdadera cuadratura del círculo es, en última instancia, imposible, por la “diferencia de especie” que separa a la línea curva del círculo de las líneas rectas de los polígonos, como vimos en el recuadro 1. La cubicación de la esfera está relacionada, de cierto, con este problema; pero, en tanto que el número de polígonos que pueden inscribirse en un círculo es infinito, hay un número limitado de sólidos que pueden inscribirse en la esfera (ver figura 1).
Luego LaRouche pide un cilindro y un cono, “cada uno con la capacidad de contener esa misma cantidad [de agua] o de duplicarla en el caso del cilindro”.
Esto exige determinar las relaciones entre el cubo, la esfera, el toro, el cilindro y el cono (ver figura 2). Quizás tú, como algunos de nosotros, fuiste entrenado en la escuela y puedes declamar las fórmulas para el volumen de la esfera, el cilindro y el cono como una respuesta pavloviana. A lo mejor no pudiste ni contenerte mientras apenas se planteaba el problema. De ser así, búscate a un incrédulo o, mejor aun, haz acopio de incredulidad y considera esta paradoja: nos dicen que el volumen del cono es menos de la mitad que el del cilindro (ver figura 3). (Lo divertido estriba en descubrir qué tanto menos).
| FIGURA 1. |
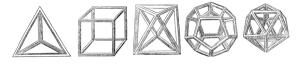 |
Estos sólidos platónicos que Leonardo da Vinci dibujó, son los únicos sólidos regulares que pueden construirse dentro de una esfera, y señalan una diferencia decisiva entre las superficies y los volúmenes. (Para que entiendas a cabalidad lo que queremos decir, trata de bisecar los lados del octaedro para construir un sólido con 16 caras, del modo que bisecarías los lados del octágono para construir un polígono con 16 lados). Advierte también que debido a su “regularidad”, a la igualdad de sus lados, el cubo es “esférico” (veremos más de esto en un momento). |
| FIGURA 2. |
|
 |
El lado del cubo es igual al radio y la altura tanto del cono como del cilindro, y al radio de la esfera (pedimos una disculpa, porque el toro brilla aquí por su ausencia). |
| FIGURA 3. (a) |
(b) |
 |
 |
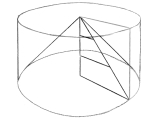
Un cilindro (a), y el cono que cabe dentro de él (b). El cono tiene la misma base y altura que el cilindro.
|
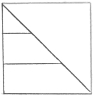
Pero, como señalará el incrédulo, el cilindro puede generarse como un volumen de rotación, el efecto de rotar un rectángulo sobre un eje que coincida con su lado. Si cortas ese rectángulo en dos por su diagonal, obtendrás un triángulo rectángulo con la mitad del área del rectángulo original (ver figura 4).
En base a eso, la “razón” nos lleva a la conclusión de que el volumen del cono será exactamente la mitad que el del cilindro. Claro que la razón aquí empleada no es sino la “razón perezosa” que Sócrates rechaza con desdén en el Fedón, o la dejadez que ridiculiza Eratóstenes, del dramaturgo cuyo personaje afirma que la tumba de cierto rey es demasiado pequeña, y que, por ende, debiera construirse del doble del tamaño doblando la longitud de cada lado. Por supuesto, nos dice Eratóstenes, eso es un craso error, pues el volumen sería ahora ocho veces mayor, cosa que el dramaturgo sabría de haberse tomado el tiempo para pensarlo.
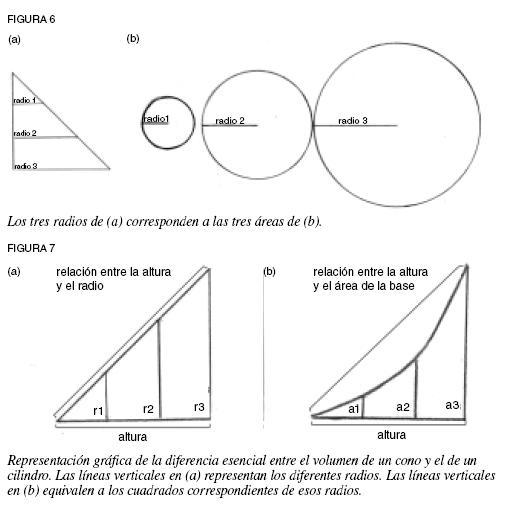
Ahora considera el cono: piensa en él como la suma de una serie de cilindros; esto equivale al método exhaustivo que mencionamos antes (ver figura 5). Los radios de la serie de cilindros cada vez más pequeños cambia en proporción aritmética en relación con el número de cilindros elegidos, pero las áreas de sus bases y, en consecuencia, sus volúmenes, cambiarían como el cuadrado de ese radio (ver figura 6).
El volumen del cono cambia de forma no aritmética, lo que hace que la relación entre el volumen de rotación del triángulo y el rectángulo, entre el cono y el cilindro, sea diferente de la que existe entre las áreas del triángulo y el rectángulo (ver figura 7). Ésta es otra diferencia entre las superficies y los sólidos con la que tenemos que bregar.
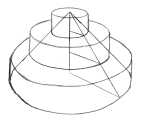
La relación entre el cilindro y la esfera puede educirse de modo parecido. Primero construye un cilindro con un radio igual al de la esfera, y una altura igual al diámetro de la misma (ver figura 8). Entonces pésalos (advierte que esto sólo funciona si están hechos del mismo material) y compara sus pesos. Pregúntate: ¿por qué esto es cierto? ¿Por qué obtuvimos este resultado? Esto arroja más luz al problema.
Pero luego te acuerdas, como de algo casi olvidado, ¡que ahora tenemos que construir una esfera, un toro, un cono, un cilindro y un cubo con el mismo volumen! Aunque está relacionado con la exploración anterior, esto añade un elemento nuevo de qué preocuparnos (ver figuras 9y 10).
Ahora llegamos al problema de doblar estos volúmenes, y del efecto geométrico de hacerlo. Hay tres formas de doblar el volumen de un sólido rectangular (ver figura 11). Esto también es cierto para el cilindro y el cono (ver figura 12). En las imágenes que se ven en la figura 13, sólo uno de los tres volúmenes doblados es similar al primero.
De manera parecida, sólo hay una forma de doblar la esfera, pues siempre tiene que ser similar a cualquier otra esfera (sopesa por un momento las implicaciones de esto). El cubo tiene que ser similar a cualquier otro cubo, así que, en este sentido, es un sólido esférico. Regresa al problema de construir volúmenes con la misma capacidad.
| FIGURA 8 |
|
 |
Aquí tenemos un cilindro cuya base tiene un radio igual al radio de la esfera, y cuya altura es igual al diámetro de la esfera. |
FIGURA 9
|
|
 |
Todos estos sólidos tienen el mismo vol umen, como lo determina el volumen de la esfera (de nuevo, disculpa la ausencia del toro). Pregúntate: ¿Cómo determinamos estos volúmenes? Cada uno plantea un problema particular de cómo encontrar una raíz cúbica. ¡Descubrir el volumen del cubo fue casi imposible! |
| FIGURA 10 |
|
 |
Los cuatro sólidos de la izquierda tienen el mismo volumen. Los sólidos originales aparecen a la derecha. En el conjunto original de sólidos, tanto el cilindro como el cono tienen un radio y una altura iguales al radio de la esfera, y el lado del cubo es igual al radio de la esfera. Nota la diferencia drástica en el tamaño de los dos cubos y de los dos conos. Las dos esferas son del mismo tamaño.
|
| FIGURA 11 |
|
 |
|
| Nuestro cubo original, cuyo lado es igual al radio de nuestra esfera, aparece hasta la derecha. A su lado aparece un sólido rectangular cuyo ancho es el doble del que tiene el cubo, en tanto que su altura y su grosor son iguales a los del cubo. El segundo sólido desde la izquierda tiene un cara que es el doble de la del cubo original, pero su grosor es igual al del cubo. Estos dos sólidos tienen un volumen del doble del que tiene el cubo original, y su construcción no requirió que encontráramos una raíz cúbica. Pero el último sólido hasta la izquierda es el cubo doblado. Su construcción requirió una profunda adición a nuestro conjunto de capacidades. |
| FIGURA 12(a) |
(b) |
 |
 |
| Tanto en (a) como en (b) el volumen original aparece en el extremo derecho, y el doble perfecto del volumen similar en el extremo izquierdo. En (a) cada uno de los tres conos que están enseguida del original tienen el doble de su volumen. El segundo de der. a izq. se dobla doblando la altura, el segundo, doblando el área de la base. El cono en el extremo izquierdo se dobló con aumentos iguales de su base y de su altura, lo que generó un cono similar. En (b) mostramos los mismos resultados para el cilindro. La base del segundo cilindro desde la izquierda (visto de canto) es del doble. |
| FIGURA 13 |
|
|
| Aquí mostramos cada sólido original con su compañero similar del doble de capacidad. Debido a la dificultad que plantea la construcción de recipientes huecos, nos dimos cuenta de que si construíamos nuestros sólidos como era debido, podíamos aprovechar un descubrimiento de Arquímedes para determinar sus volúmenes. |
Hay modos de hacer trampa al construir un cono o un cilindro con un volumen igual al de una esfera. Si no te importa que los sólidos que generes sean similares a tus objetos originales, el problema es tan simple como cambiar la altura o el área de la base del original. Pero entonces te pierdes la diversión de enfrentar la construcción de una serie de raíces cúbicas diferentes. Aun si tratas de eludir esta dificultad, no puedes escapar del problema de encontrar una raíz cúbica (y una muy extraña por cierto) cuando construyes un cubo con la misma capacidad de la esfera.
En este experimento con volúmenes, que es en esencia un estudio de los cubos, el problema de lo curvo y lo recto acecha a cada esquina (y a cada arista). Cuando en su Óptica Kepler habló de la relación que existe entre las funciones cónicas, considerando las diferentes secciones cónicas como una transformación continua de lo perfectamente curvo, el círculo, a lo perfectamente recto, la línea recta, en verdad estaba describiendo los aspectos de lo curvo y lo recto que se unen en el propio cono (ver figura 14).
A este respecto, el cono y el cilindro obviamente comparten esta importante característica, esta unión de lo curvo y lo recto, como se aprecia en sus secciones (ver figura 15).
Pero el cubo, que no parece tener nada de curvo, ¡es en sí esférico! (ver figura 16).
Para concluir, considera el caso del toro, tan desatendido en esta presentación inicial. ¿Dónde pertenece? Y, por fin, ¿cómo es que se construyen esas raíces cúbicas?
| FIGURA 14 (a) |
(b) |
 |
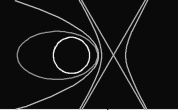 |
| En (a) mostramos las diferentes secciones cónicas en progresión desde el corte horizontal —el cual genera el círculo del extremo derecho—, a un corte menos que paralelo con el lado del cono —que resulta en una elipse—, a un corte paralelo con el lado —que nos da la parábola—, a un corte entre el ángulo del lado y el vertical —el cual produce la hipérbola—. El corte final es aquél realizado por el eje de rotación, que revela el triángulo que se rota para generar el cono. En (b) mostramos un diagrama que Bruce Director diseñó para demostrar el concepto de Kepler de las funciones cónicas. Conforme el foco se mueve hacia la izquierda, el círculo se convierte en una elipse. En el límite con el infinito, la elipse se convierte en una parábola. La hipérbola se forma del “otro lado” del infinito. |
| FIGURA 15 |
|
 |
Aquí mostramos que sólo existen tres cortes diferentes del cilindro, ¡no importa cómo lo cortes! (El corte axial que genera un rectángulo no aparece). Nota que el cilindro y el cono comparten los cortes circular y elíptico (aunque en el cilindro todos sus cortes elípticos son de una clase especial), pero la parábola y la hipérbola son exclusivas del cono. |
| FIGURA 16 |
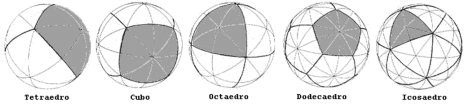 |
| de izq. a der.: tetraedro, cubo, octaedro, dodecaedro, icosaedro |
— Todo el Movimiento de Juventudes Larouchistas en Seattle, EU participó en este proyecto. Además de Niko Paulson, Peter Martinson y Rianna St. Classis, Dana Carsrud y Will Mederski ayudaron sin cejar al progreso de este proyecto hasta su fase actual; ayudaron a construir las herramientas para construir los sólidos y en la propia construcción de los mismos, a pintarlos, cubrirlos de resina y fotografiarlos. ¡Y ahora todos jugaremos con ellos! Lora Gerlach, Will Mederski, Dana Carsrud y Riana St. Classis tomaron las fotografías. Lora Gerlach también aportó su invaluable ayuda navegando por las llanuras digitales de Photoshop y Word.
— Traducción de Carlos Cota Moreno, miembro del Movimiento de Juventudes Larouchistas en México.