|
Resumen electrónico de EIR, Vol.XXIII, núm. 4-5
|
|||||||||||||
|
Recuadro 4: Cardano y las raíces complejas Lea El principio del ‘poder’ en formato PDF
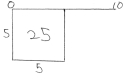
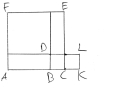
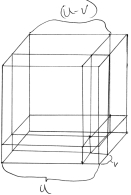
Arquitas realizó un acto prometeico cuando descubrió una solución guiada por la esférica a la paradoja de vida o muerte de cómo doblar el cubo. Para Arquitas, esa solución no yace en el dominio visible del propio cubo, sino que pertenece a un dominio superior en el que la creatividad humana danza con los principios universales que Gauss posteriormente ha llamado el dominio complejo. De entonces a la fecha, esos herederos del legado de Aristóteles y Euclides que pretenden robarle su fuego al hombre a nombre de sus amos oligarcas, y remplazarlo con fórmulas analíticas desalmadas, han perpetrado acciones desdeñosas una y otra vez contra Arquitas. Fue más de 1.100 años después de Diofante, el padre griego del álgebra que había foprmulado sus matemáticas en la menguada tradición de los pitagóricos, que Jerónimo Cardano planteó por primera vez (al abordar el problema de cuadrar y cubicar) la idea de las raíces complejas en tanto soluciones formales a problemas algebraicos. Por ejemplo, si dada la ecuación x2-10x + 40, las leyes del álgebra establecen que para una ecuación con coeficientes racionales, el primero de ellos (o sea, 10) será la suma de las soluciones, y el último (o sea, 40), el producto de esas soluciones. Para el apostador notorio Cardano, siguiendo la tradición empírica de al–Jwarizmi (famoso por la noción de completar el cuadrado), esto se convierte en un problema de encontrar cómo dividir una línea de 10 unidades, de modo que las dos partes multiplicadas sean igual a 40 (ver figura 1). Pero como el área más grande que puede crearse mediante este proceso (un cuadrado) tiene un área de 25, se considera que el problema es físicamente absurdo, pero soluble en lo algebraico, si permitimos números de la forma (a+b√-1); en este caso, (5+√-15) y (5-√-15). Esta clase de cantidades han venido a conocerse como imaginarias, y obsesionaron a Cardano cuando abordaba el problema físico de cubicar. A diferencia de Arquitas, quien preguntó qué acción compleja tiene el poder de generar magnitudes cúbicas, Cardano no partió de la acción, sino de la certeza sensorial de los cubos materiales y su derivado algebraico. Él planteó su problema cúbico como sigue: “Por ejemplo, digamos que el cubo de GH y seis veces el lado GH son igual a 20. Tomo dos cubos AE y CL cuya diferencia será 20, de modo que el lado AC multiplicado por el lado CK será 2 (ver figura 2)”. De aquí, la ecuación de Cardano para las soluciones generales a problemas cúbicos “se desprende” algebraicamente. Aplícale a la ecuación x3-12x =10, el método que prescribía Cardano, que de hecho es puramente analítico, a pesar de que pide empezar por trazar el diagrama de un cubo (ver figura 3): Si tenemos u3-v3 = 10 and u3 X v3= -64, y, por consiguiente, u X v = -4. Y como uv = -4, then 12(u-v) = 12(u-v). Y puesto que u3 = 10+v3 = 10+64/u3, y como u3v3 = -64, entonces tenemos u6 = 10u3+64: una cuadrática que puede resolverse usando la centenaria fórmula cuadrática (que se deriva con facilidad del trabajo que realizó al–Jwarizmi para completar el cuadrado): -b/2a ± √(b2-4ac)/2a. Usando esa fórmula, arribamos a las soluciones “imaginarias”:
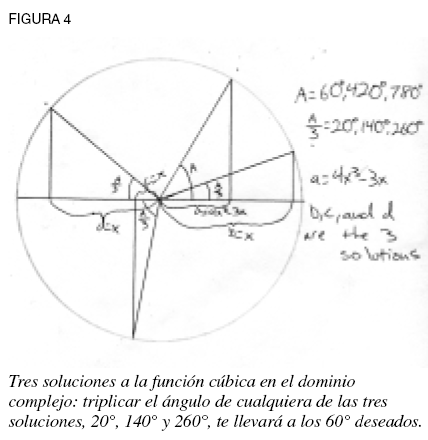
De nuevo, el álgebra, aplicada a lo que en realidad es un problema físico, ha generado algo ambiguo e incognoscible. Al realizar investigaciones algebraicas de cuadrados y cubos literales, la ocurrencia de cantidades complejas como soluciones es toda una paradoja. Porque, ¿qué es un cubo negativo en el mundo material? (¿Es 3√-x la arista de un cubo cuyo volumen es -x?). Y, aun más absurdo, ¿cómo “se vería” algo como x4 o x5, etc.? Así, la geometría, cuando se le condena al espacio euclidiano tridimensional de una “Tierra plana”, pierde el nombre de acción, adoptando el carácter de un cadáver tieso que ya no es susceptible de interactuar cognoscitivamente; y el álgebra se convierte en una seudociencia que se practica para mantener una fantasía de “torre de marfil”. Fue en continuación de esta tradición depravada, que parece que un aliado íntimo y coconspirador de Sir Isaac Newton, Abraham de Moivre (cuyo trabajo principal era de consejero de los apostadores de su tiempo, muy parecido a la mayoría de los matemáticos actuales que trabajan para los diferentes fondos especulativos —que parecen casinos— de Wall Street), fue el primero que halló conveniente aplicar las leyes trigonométricas (aunque sin conexión alguna con la acción circular de la que nacieron dichas leyes) a su sádica investigación de las raíces cúbicas. En una tentativa en particular, empieza con lo que llama un “binomio imposible” (a +√-b), y trata de encontrar sus raíces cúbicas. A sabiendas, por su intenso adoctrinamiento en los libros de texto de matemáticas, que la ecuación trigonométrica 4cos3A/3 - 3cosA/3 = cosA, relacionada con la trisección de un ángulo, puede llevarse a tres soluciones, se propuso torcer la ecuación algebraica, para un binomio al cubo (x + √-y)3 = x3 +3x2√-y -3xy -y√-y a una forma algebraicamente afín a la de la fórmula trigonométrica (esto es, 4x3 - 3mx = a = 4(x/r)3 - 3(x/r) = c/r = 4x3 - 3r2x = r2c). Una vez logrado esto, De Moivre efectúa una serie de manipulaciones algebraicas de la ecuación trigonométrica, termina con tres soluciones angulares, “aplica la tabla de los senos”, y obtiene tres nuevas fracciones que luego enchufa de vuelta a su ecuación algebraica antes derivada, lo soba un poco, y termina con las tres soluciones algebraicas deseadas, dos de las cuales son “imaginarias” (a +√-b). Así que, como Cardano, termina con magnitudes algebraicas que, de cuadrarse, se diría que han producido un área negativa; una paradoja, y en este caso doble, pues esto se logró usando funciones circulares (trigonométricas). Pero para De Moivre, cuya creatividad la mutiló ese abuso de “dale y machaca” a manos de sus controladores de “torre de marfil”, no hay ninguna paradoja. El hecho de que sus investigaciones algebraicas lo lleva a usar funciones circulares, donde z = x + iy se convierte en z = r(cosφ + isenφ), y encontrar la raíz cúbica adopta la forma de descubrir la raíz cubicada de un radio (3√r) y la trisección del ángulo (φ/3), es sólo significativo en lo formal e incognoscible en lo ontológico. Para De Moivre no hay una acción ni principios ordenadores superiores en juego, sólo la idea del mundo de sombras “imaginario” del álgebra y sus “respuestas correctas”. Por desgracia, como estaba obsesionado, o mejor, poseído por el álgebra formal, y debido a su negación absoluta de que los principios de acción característicos de la geometría constructiva son cognoscibles, la ocurrencia paradójica de raíces complejas y su manejo mediante propiedades trigonométricas nunca movieron a De Moivre a hacer esas preguntas de causa que engendraron la hipótesis que planteó Gauss, de que las “imaginarias” eran reflejo de una acción ontológicamente trascendental. Fueron los grilletes mentales que le impuso el formalismo algebraico los que le impidieron buscar la geometría física trás las sombras de sus fórmulas, para descubrir que lo que había considerado “imposible” eran de hecho los efectos de una acción física verdadera. Por ejemplo, en la construcción física de la trisección del ángulo, dos de las soluciones que a De Moivre le hubieran parecido imaginarias, son de hecho reales (ver figura 4).
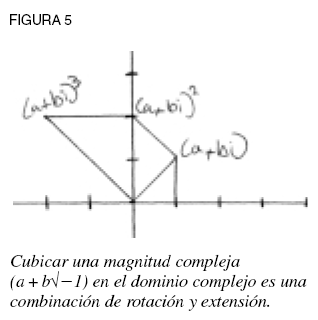
En otras palabras, los números complejos no son cantidades aritméticas, sino más bien los escondites de una acción superior cognoscible que subsume al álgebra. Así, a Gauss le correspondió reavivar la llama de la esférica pitagórica a la que esos seguidores de la secta de Newton habían reducido a cenizas latentes (ver figura 5).
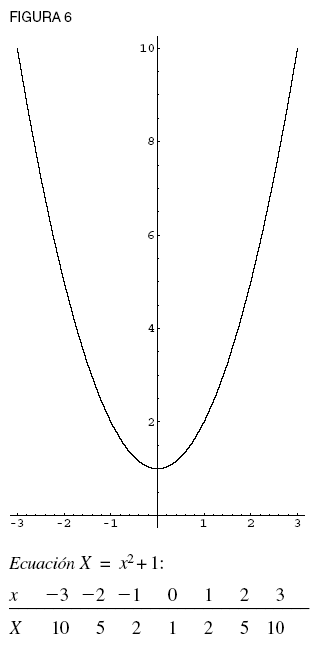
Fue uno de los alumnos de De Moivre, D’Alembert, quien pensó que podía purgar la geometría completamente de la ciencia al aparentar introducirla en su intento de probar el teorema fundamental del álgebra. En efecto, usó lo que se podría llamar el método de “enchufar y ver qué pasa” de la graficación cartesiana de los puntos en el plano, de tratar de irte acercando a infinito a la solución. Así, dado el problema algebraico x2+1 = 0, el método de D’Alembert pide simplemente probar todos los valores reales posibles para la variable, y graficar la variable como la ordenada y la función como la abscisa (ver figura 6).
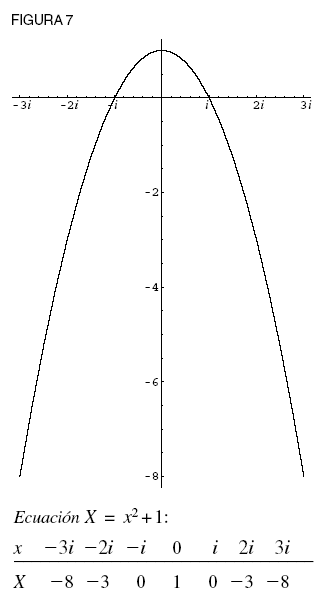
Para los casos en los que los reales no llevan a una respuesta, tal como en el problema x2+1 = 0 D’Alembert invoca la magia de las imaginarias, y dice que podemos usar cantidades de la forma a + b √-1 para producir soluciones. Si probamos todas las cantidades a + b √-1 posibles, generamos una curva que cruza la ordenada imaginaria, lo que nos da nuestras dos respuestas (ver figura 7).
Ante esto, Gauss dice de la prueba de D’Alembert: “Es correcto observar que D’Alembert aplicó consideraciones geométricas en la exposición de su prueba, y consideró a X como la abscisa y a x como la ordenada de una curva. . . pero todo su razonamiento, si uno sólo considera lo esencial, no descansa en principios geométricos, sino en los puramente analíticos, y una curva y una ordenada imaginarias son conceptos más bien difíciles y pueden ofender a un lector de nuestros tiempos”. Éste es el quid del ataque de Gauss a la suma de las obras de Euler, D’Alembert y demás en su prueba de 1799 del Teorema fundamental del álgebra: en sus pruebas la geometría constructiva y, por ende, la creatividad humana, brillaban por su ausencia. A lo más, ellos simplemente investigaron lo que es, en vez de preguntarse: ¿qué tiene el poder de hacer posible lo que es? No es una hipérbole decir que esta pelea sobre el reto de descubrir una solución a la paradoja asociada con doblar el cubo es de vida o muerte. Como lo ha demostrado la historia, y como el descubrimiento de LaRouche ha dado a conocer, el hombre sólo sobrevive cuando progresa, y sólo progresa cuando aplica su facultad única humana de la cognición a aquellas paradojas que el universo nos comunica. La geometría constructiva, en el dominio complejo, de la tradición de Arquitas, pasando por Gauss y Riemann, encarna aquellos actos creativos que no sólo expresan, sino que también fortalecen esa relación entre el hombre y el universo. Cualquier intento de formalizar y degradar tales problemas universales de la geometría física al nivel de lo analítico, es nada menos que un crimen de lesa humanidad cometido en el interés de aquéllos a quienes Dick Cheney llama amos. —Cody Jones y Chase Jordan.
|
||||||||||||||