|
|
|
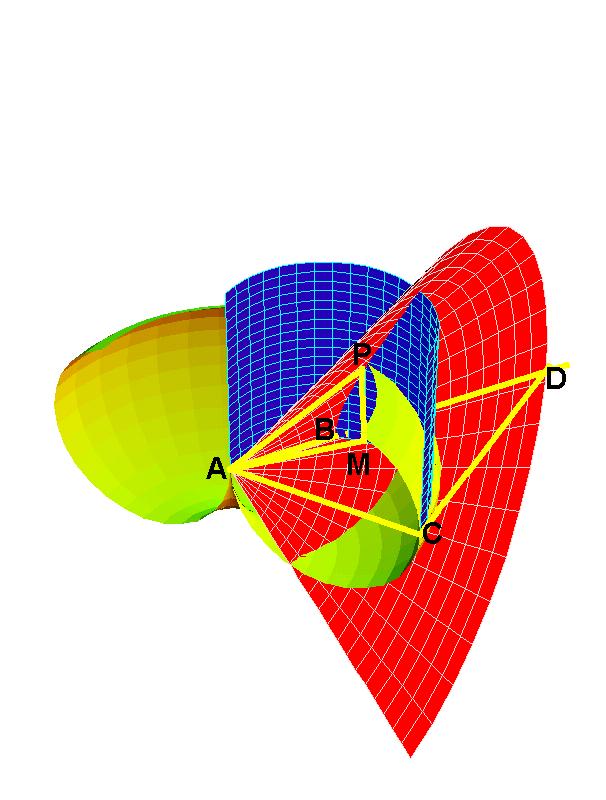
- 2(b) This is a "cut-a-way" view of 2(a). M is found by dropping a line from P until it intersects the plane of the cylinder that includes AC. Archytus demonstrated that AM is the smaller mean between AB and AC, and AP is the longer mean. Thus, AB : AM :: AM:AP :: AP:AC. So, if AB = 1 and AC = 2, then AM = 21/3 and AP = 22/3 .
|
|
|